WinForm/C# 时间复杂度和空间复杂度以及空间换时间小例
时间复杂度和空间复杂度
通常不同的算法虽然结果一样但是消耗资源和时间却会有很大差别,衡量不同算法之间的优劣就要用到时间复杂度和空间复杂度
时间复杂度
时间指运行算法所需要的时间,那我们运行用 C# 程序看一下运行时间不得了,但是这个性能好的电脑和性能不好的电脑时间肯定是不同的。所以有了大 O 符号表示法 T(n)=O(f(n))
下面这个 for 循环运行需要
for (int i = 0; i < n; i++) 需要一个单位时间
j = i;N 次需要 N 个单位时间
j++;也是 N 次
所以时间复杂度为 T(n)=(1+2n)* 单位时间
简化为 O(n)
for (int i = 0; i < n; i++)
{
j = i;
j++;
}
常见的时间复杂度量级
-
常数阶 O(1)
就是没有复杂循环结构 不管执行多少行几万十几万行都按 O(1) 算
j = i; j++; -
线性阶 O(n)
就是上面的 for 循环 消耗时间随着 N 变化而变化
for (int i = 0; i < n; i++) { j = i; j++; } -
对数阶 O(logN)
下面的循环就按 i*2 何时=N,就是 2 的多少次方是 N,log2^N
int i = 1; while(i<n) { i = i * 2; } -
线性对数阶 O(nlogN)
就是 for 循环套 while
for(m=1; m<n; m++) { i = 1; while(i<n) { i = i * 2; } } -
平方阶 O(n²)
就是双重 for 循环 如果把里面一层改成 m 那么复杂度就是 O(m*n)
for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { j = i; j++; } }
然后 for 越多就 K 次方阶 O(n^k) 这样子
空间复杂度
-
O(1)
就是算法执行临时空间不会随着 N 发生变化 都算成一个常量
j = i; j++; -
O(n)
int[] m = new int[n] new 出来了 N 个所以是 N 下面循环并没有再开临时变量
int[] m = new int[n] for(i=1; i<=n; ++i) { j = i; j++; }
空间复杂度其实和时间复杂度判断标准差不多主要是看开了多少个临时变量是否跟 N 有一定的线性关系
这都是一些简单的如果是复杂的怎么计算呢 下面都计算时间复杂度为例子
- T(n) = n + 29 一般说是 O(n) 因为常数项影响函数增长很小
- T(n) = n^3 + n^2 + 29 一般说为 O(n3),n3 的增长速度是远超 n^2 的,同时 n^2 的增长速度是远超 n 的,所以有了高次项可以忽略低次项
- T(n) = 3n^3 一般说为 O(n^3) 因为阶数比乘数影响增长速度最显著我们通常忽略
比如这个时间复杂度为 max(O(n^2), O(n)) 及 O(n^2)
void aFunc(int n) {
// 第一部分时间复杂度为 O(n^2)
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf("Hello, World!\n");//时间复杂度为O(1)
}
}
// 第二部分时间复杂度为 O(n)
for (int j = 0; j < n; j++)
{
printf("Hello, World!\n");
}
}
下面这个 T(0)=T(1)=1
T(n)=T(n-1)+T(n-2)+1 加一因为加法算一次执行
会发现这就是个裴波那契数列
long aFunc(int n) {
if (n <= 1) {
return 1;
} else {
return aFunc(n - 1) + aFunc(n - 2);
}
}
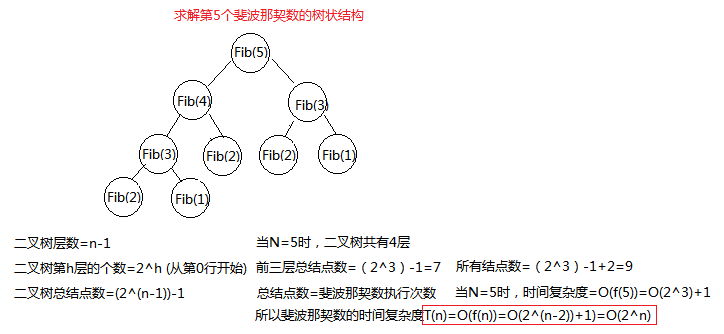
就是每多一层计算就要一次单位时间
就按第五层来算就是 2^3+1=7 次计算
N 才需要 2^(n-2)+1 次计算
那么时间复杂度就是 O(2(n-2)+1)常数项忽略就是 O(2n)
空间换时间案例
在执行多次循环时,可以通过键值对的方式替换循环。达到空间换时间,提高运行效率。
#region 获取两个数组中名称相同的值的和
#region 写法一
DateTime time1 = DateTime.Now;
int sum1 = 0;
int num1 = 0;
foreach (var class1 in class1s)
{
foreach (var class2 in class2s)
{
if (class1.Name == class2.Name)
{
sum1 += class1.Value + class2.Value;
}
num1 += 1;
}
}
DateTime time2 = DateTime.Now;
Console.WriteLine($"写法一:总和为{sum1},循环{num1}次,耗时:{(time2 - time1).TotalMilliseconds}毫秒");
#endregion
#region 写法二
DateTime time3 = DateTime.Now;
int sum2 = 0;
int num2 = 0;
foreach (var class1 in class1s)
{
foreach (var class2 in class2s)
{
num2 += 1;
if (class1.Name == class2.Name)
{
sum2 += class1.Value + class2.Value;
break;
}
}
}
DateTime time4 = DateTime.Now;
Console.WriteLine($"写法二:总和为{sum2},循环{num2}次,耗时:{(time4 - time3).TotalMilliseconds}毫秒");
#endregion
#region 写法三
DateTime time5 = DateTime.Now;
int num3 = 0;
Dictionary<string, int> pairs = new Dictionary<string, int>();
foreach (var class2 in class2s)
{
pairs.Add(class2.Name, class2.Value);
num3 += 1;
}
int sum3 = 0;
foreach (var class1 in class1s)
{
if (pairs.ContainsKey(class1.Name))
sum3 += class1.Value + pairs[class1.Name];
num3 += 1;
}
DateTime time6 = DateTime.Now;
Console.WriteLine($"写法三:总和为{sum3},循环{num3}次,耗时:{(time6 - time5).TotalMilliseconds}毫秒");
Console.ReadLine();
#endregion
#endregion
